Geometry
约 1567 个字 94 行代码 1 张图片 预计阅读时间 9 分钟
Introduction
隐式几何: \(f(x,y,z)=0\)
使用隐式表示,可能难以想想图形长什么样;但是很方便判断某一点是否在图形上
显式几何:直接给出或通过参数映射给出各个点(或小三角形)的坐标
对于同样一个几何形体(y和z调换一下):

Implicit
Constructive Solid Geometry

Distance Functions
对每个点维护它们离几何图形最近的距离,当两个图形需要 Blend 时,将 Signed Distance Function 相加以更新:

当我们对两个几何形体进行 Blend 时,面上某个点的距离函数更新为其对分别两个图形的距离函数的相加,则融合后的几何形体的边界为新的距离函数等于0的点。

Level Set Methods
与距离函数类似,但是是每个格子维护一个相对高度。

Fractals
即分形,可以类比算法中的递归,用来描述自相似的几何图形,但是较难控制形状。
比如雪花。
Explicit
Point Cloud
用一组点表示几何图形,点云密度足够大才能表示一个较为复杂的模型。
在实际应用中通常需要转换为三角形面。
Polygon Mesh
多边形面表示是图形学中使用最广泛的显式几何,非常方便进行处理、仿真、采样等操作。
在 Wavefront Object File (.obj) 中,多边形面的格式如下:
| v 0.23639098 17.838633 1.3139851 # 顶点坐标
vt 0.499264 0.29569197 0 # 纹理坐标
vn 0.41076726 0.49810898 -0.76364768 # 法线
f 12/11/15 12/11/15 12/11/15 # 连接关系,face
# 例如 12/11/15 指第12个v,第11个vt,第15个vn为一组
# 在Unity中相当于Mesh类的indices数组
|
Bezier Curves
贝塞尔曲线使用一系列控制点来定义一段曲线。
先考虑只有三个控制点的二阶贝塞尔曲线(quadratic Bezier):

其中 \(\frac{b_0 b_0^1}{ b_0 b_1} = \frac{b_1 b_1^1}{b _1 b_2} = \frac{b_0^1 b_0^2 }{b_0^1 b_1^1} = t\)
数学上,易证明得到(上标表示层数,不是平方):
\[\begin{array}c b_0^1(t) =(1-t)b_0 +tb_1 \\ b_1^1(t) =(1-t)b_1 +tb_2 \\ b_0^2(t) =(1-t)b_0^1 +tb_1^1 \\ \Rightarrow b_0^2 = (1-t)^2b_0 +2t(1-t) b_1 +t^2b_2 \end{array}\]
同样适用于更多点数:

那么有 Bernstein Form of order n:
\[\begin{array}c b^n(t) = b_0^n(t) = \sum_{j=0}^n b_j B_j^n(t) \\ B_j^n(t) = C_n ^i t^i (1-t)^{n-i} \end{array} \]
其中 \(B_j^n(t)\) 称为 Bernstein polynomial。
最常用的是有四个控制点的四阶贝塞尔曲线 Cubic Bezier
贝塞尔曲线有如下性质:
- 起点和终点满足:\(b(0)= b_0, b(1)=b_n\)
- 起点和终点的切线满足:\(b'(0)=n(b_1 -b_0), b'(1)= n(b_n -b_{n-1})\)
- 对控制点先做仿射变换再画贝塞尔曲线得到的结果与对控制点先画贝塞尔曲线再对曲线仿射变换一样(几何不变性)
- 贝塞尔曲线一定位于控制点形成的凸包内
Convex Hull
即能包围给定点的最小凸多边形
通常使用 Piecewise cubic Bezier curve (分段,每四个点,贝塞尔曲线)作为曲线描述。例如 PS 中给出的钢笔工具就是采用四个点作为控制点来画出贝塞尔曲线。

You can try in Bezier curve edit
连续性
若只是方向相同,定义为该处 C0 Continuity;若方向和距离都相同,定义为该处 C1 Continuity
用 Unity 写的一个贝塞尔曲线实现:
| public class BezierCurve : MonoBehaviour
{
public Transform[] referencePointTransforms;
public Transform curvePointTransform;
Vector3[] mReferencePoints;
int mSign = 1;
float t = 0;
int mResolution = 100;
void Update()
{
TransformsToVectors();
t = Mathf.Clamp(t, 0, 1);
// curvePointTransform.position = GetCurvePointDeCasteljau(mReferencePoints, t);
curvePointTransform.position = GetCurvePointByBernstein(mReferencePoints, t);
t += Time.deltaTime * 0.2f * mSign;
if (t > 1 || t < 0)
mSign *= -1;
}
void OnDrawGizmos()
{
TransformsToVectors();
if (mReferencePoints.Length == 0)
return;
//画控制点连线
Gizmos.color = Color.red;
for (int i = 0; i < mReferencePoints.Length - 1; i++)
Gizmos.DrawLine(mReferencePoints[i], mReferencePoints[i + 1]);
//画曲线
Gizmos.color = Color.green;
Vector3 start = mReferencePoints[0];
for (int i = 1; i <= mResolution; i++)
{
Vector3 end = GetCurvePointDeCasteljau(mReferencePoints, (float)i / mResolution);
Gizmos.DrawLine(start, end);
start = end;
}
}
void TransformsToVectors()
{
int referencePointCount = referencePointTransforms.Length;
mReferencePoints = new Vector3[referencePointCount];
for (int i = 0; i < referencePointCount; i++)
mReferencePoints[i] = referencePointTransforms[i].position;
}
}
|
使用C++ openCV 的 de Casteljau's algorithm 实现方式:
| void naive_bezier(const std::vector<cv::Point2f> &points, cv::Mat &window)
{
// Benstein basis: B_i^n(t) = C(n, i) * t^i * (1 - t)^(n - i), b^n = sum(B_i^n(t) * P_i)
auto &p_0 = points[0];
auto &p_1 = points[1];
auto &p_2 = points[2];
auto &p_3 = points[3];
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = std::pow(1 - t, 3) * p_0 + 3 * t * std::pow(1 - t, 2) * p_1 +
3 * std::pow(t, 2) * (1 - t) * p_2 + std::pow(t, 3) * p_3;
window.at<cv::Vec3b>(point.y, point.x)[2] = 255;
// Blue; Green; Red = (0, 0, 255)
}
}
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t)
{
// de Casteljau's algorithm by recursive
std::vector<cv::Point2f> points;
if (control_points.size() == 1)
return control_points[0];
cv::Point2f Pre_point = control_points[0];
for (auto iter = control_points.begin() + 1; iter != control_points.end(); ++iter)
{
points.push_back(Pre_point + t * (*iter - Pre_point));
Pre_point = *iter;
}
return recursive_bezier(points, t);;
}
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = recursive_bezier(control_points, t);
window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
}
}
|
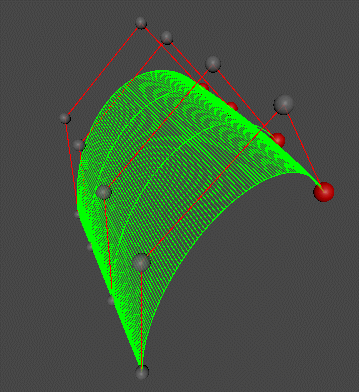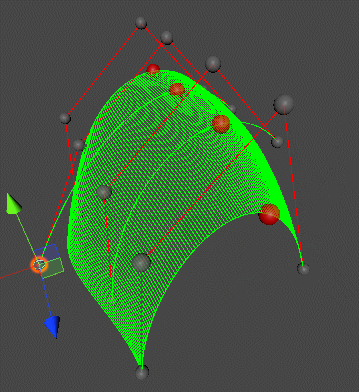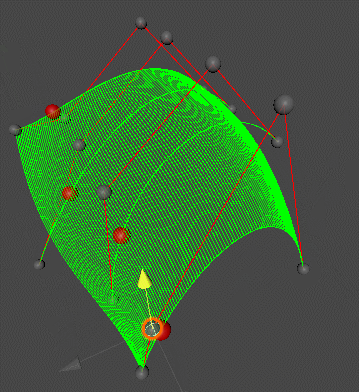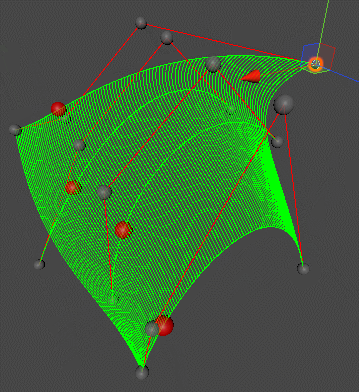
Bezier Surfaces

For bi-cubic Bezier surface patch,
- Input: 4 * 4 Control Points
- Output: 2D surface parameterized by \((u,v)\) in \([0,1]^2\)
具体做法是对每四个点都画出对应的贝塞尔曲线,再对每四个贝塞尔曲线上 \(t\) 时刻运动的四个点画出画出一个 moving curve。
Mesh Operation
- Subdivision 细分
- Simplification 简化
Loop Subdivision
Loop 细分和循环没关系,是因为算法的发明人姓 Loop

- 对于旧顶点,根据连接的旧定点数(该节点的度)选择不同的权重加权平均:

Catmull-Clark Subdivision
上述 Loop 细分只能应用于网格呈三角形的模型,而 Catmull-Clark 细分适用于更 General 的网格。
定义非四边形面为 Non-quad face ,定义度不为四的点为 Extraordinary vertex :

对每一个面取中心点,对每一条边取中点,并把这些新的点全部连接起来。那么细分之后,在 Non-quad face 中会增加一个奇异点,而所有的非四边形面均消失:

所以在之后的细分中,奇异点的个数不会增加。
坐标更新的加权平均算法如下:

Quote

Collapsing An Edge Simplification
在保留整体形状的前提下减少网格面数,从而降低性能需求。
在 Games101 课程中介绍的简化算法为边坍缩。
为了实现这个算法,我们引入二次误差(Quadric Error)的概念,其定义为一个新顶点到原本相关的三角形平面的距离的平方和。

对于整个模型,计算每一条边坍缩后造成的二次误差,而选择误差最小的边坍缩。坍缩后更新与这两个点相连的所有边的误差值,然后继续坍缩。

数据结构
该算法的一般操作为取最小值以及修改键值,所以用来存储二次误差值的数据结构应该选择优先队列。

















